Introduction
One of the most important decisions made for public sector pension plans is adopting a funding policy that balances the needs of all stakeholders. In general, larger benefits require larger contributions. For a given benefit level, the purpose of a funding policy is to balance the level and volatility of contributions with the funded status of the plan. In this article, we continue to explore, compare, and contrast various methods of amortizing liabilities and their impacts on the contribution rates allocated to employers.
The first article of this series, Public pension plan funding policy: Effectiveness of amortization methods, developed a framework to help plan sponsors understand the funding policy implications of their choice of amortization method if all actuarial assumptions are perfectly met. This article expands that discussion to focus on how the various amortization methods handle deviations from expectations. Specifically, this article looks at how the various amortization methodologies react to volatility in investment markets. We selected these particular amortization methods as they are the most commonly used. This is not an exhaustive list of funding methodologies. A plan should use the methodology that best meets the needs of its stakeholders.
Figure 1: Employer contributions (500th scenario)
Plan modeled
For purposes of this article, we modeled a “typical” ongoing open public pension plan. We use a 7.0% expected return on assets, which is a common assumption among public pension plans, an entry age normal actuarial cost method, and a fresh start for the amortization of the unfunded liabilities. We then explored multiple amortization methodologies. We set assets equal to 79% of liabilities, which is the aggregated funding level in the Milliman Public Pension Funding Index (PPFI) as of January 1, 2021. Additional key methods, assumptions, and plan provisions are listed in our appendix.
Stochastic modeling
In this article we focus on volatility inherent in investment markets. Therefore, we developed 1,000 “random walk” scenarios for the plan’s actual asset returns via stochastic projections using a random number generator, the plan’s asset allocation, and Milliman’s capital market assumptions. “Stochastic testing” involves using a random number generator to perform a statistical analysis where 1,000 or more runs are created to test the likelihood of future events. This is also sometimes referred to as Monte Carlo analysis. In our projections, other than the actual investment returns, we assume that all assumptions are met and that there are no other actuarial experience gains or losses.
The stochastic testing in this article consists of asset return projections over the 40-year period generated using a normal distribution, a 7.00% geometric average annual return, and a standard deviation of 12.00%. The equivalent average arithmetic return is 7.72%.
Throughout the remainder of this article, we look at how each of the amortization methods reacts to sample scenarios from the stochastic projections.
Results under a single scenario
Often, stochastic testing is used to create a “cone of uncertainty.” This valuable tool for risk analysis will be explored in a later article in this series. One limitation of cones of uncertainty is the illusion of smoothness. Therefore, before exploring cones of uncertainty, we focus on the path of single scenarios. As shown throughout this article, the path of a single scenario can be quite volatile and provides insight into how the various amortization methods handle asset volatility.
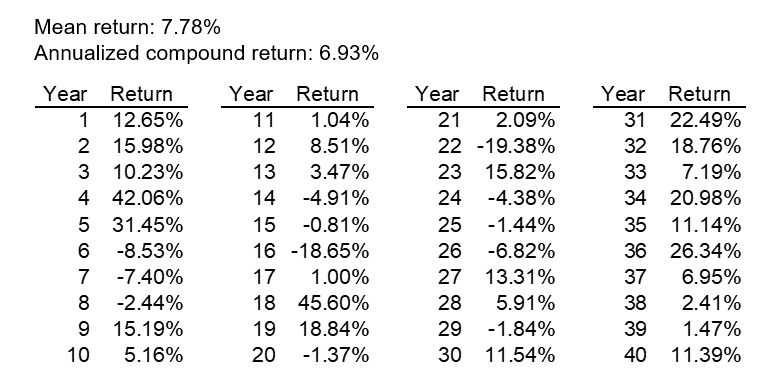
We examined each amortization method under a single scenario selected from the stochastic projections. When the scenarios are ordered from lowest to highest based on the cumulative return over the 40-year projection period, we selected the 500th scenario and define it as the “median.” This median scenario had an annualized compound return of 6.93%, slightly less than the 7.0% expected. Details of the scenario, including the annual returns, can be found in the appendix.
Funded status
The funded status under different amortization methods over the 40-year projection period for the median scenario are shown in Figure 2. The funded status here is the actuarial value of assets as a percentage of the total pension liability. The actuarial value of assets is a smoothed asset value, based on the market value of assets, but recognizing gains and losses over five years. This smoothing reduces the volatility of the funded status.
Figure 2: Funded status (500th scenario)
The funded status behaves similarly under the different methods. However, near the end of the projection period, the funded status begins to differentiate.
There are two broad generalizations we can make when the funded status is below 100% and all assumptions are met. First, shorter amortization periods lead to a higher funded status. Second, layered funding methods will lead to a higher funded status compared to a rolling method with the same amortization period.
In this scenario, due to the high initial returns, the funded status reaches 100% by year 6 under all methods and maintains a funded status above 100% through year 15. However, over the next 15 years, the funded status deteriorates under all methods, and dips below 50% under Rolling-30 and Layered-30 methods. For the last 10 years of the projection, years 30 to 40, the funded status then improves again under all methods due to the high average returns during this period.
Layered-15 and Layered-20 end up with the largest funded status at the end of the period, while Rolling-30 and Layered-30 end up with the lowest funded status. There is a 51% spread between Layered-15 (the highest funded status at 140%), and Rolling-30 (the lowest funded status at 89%). Rolling-30 and Layered-30 don’t recover to 100% at the end of the 40-year projection period despite effectively reaching the expected 7% return and having reached well over 100% funded early on in this scenario.
If all assumptions are perfectly met with precisely 7% investment earnings each year, Rolling-30 would end the 40-year projection period at 89% funded, as seen in Public pension plan funding policy: Effectiveness of amortization methods. The slow reactions of the long amortization periods may be reason for some employers to move to a shorter amortization period. Note that recent funding guidance from both the Society of Actuaries’ Blue Ribbon Panel on Public Pension Plan Funding | SOA and the Conference of Consulting Actuaries' Actuarial Funding Policies and Practices for Public Pension Plans (ccactuaries.org) specifically caution against long, rolling amortization periods.
The purpose of analyzing this scenario is to highlight the volatility that can occur under different amortization methods, assuming no benefit changes, or changes to the funding or investment policies. However, were this a real plan, the funded status under all methods is so high from years 7 to 9, at 125% or higher, that it’s possible there would be an increase in benefits provided1 or changes to the funding or investment policy. Depending on the nature of the benefit changes during good times, the low funded status and high contributions in the following 10 to 20 years could be worse.
A note on actuarial versus market value of assets
If the funded status were instead measured as a percentage of the market value of assets, rather than the smoothed value used above, there would be more volatility. Figure 3 shows the funded status on a market value basis (i.e., market value of assets as a percentage of the actuarial accrued liability) by year for the same median scenario.
Figure 3: Funded status MVA basis (500th scenario)
Employer contributions
The funded status under various amortization methods may move similarly, but employer contribution rates show striking differences between methods, particularly in the second half of the projection. Before the initial layer is eliminated under the layered methods, rolling and layered methods move similarly, although methods with shorter amortization periods experience more volatility. At years 15, 20, and 30, the respective layered methods all have a drop in the contributions. From this point on, the layered methods are more volatile than the rolling methods.
Figure 4: Employer contributions (500th scenario)
The volatility under layered methods, particularly when paired with shorter amortization periods, may be challenging for plans sensitive to volatility in employer contributions. For example, under Layered-15, the contribution rate increases from 0% to 38% in just 10 years, from years 16 to 25. Under Layered-20, the contribution rates increase from 8% to 42% over a seven-year period, from years 23 to 29, then drop back to 0% over the next 10 years.
Figure 5: Contribution rates
The average employer contributions are 13.7% under both Layered-30 and Aggregate methods over the 40-year period. However, the funded status at the end of the projection period is 97% under Layered-30, and 123% under the Aggregate method. This is primarily due to the relative responsiveness of the Aggregate method, which created a higher funded status headed into the favorable return years 30 to 36.
The largest one-year and five-year increases in contribution rates may be challenging for some plans to manage, particularly under Layered-15 and Layered-20, where the increases are the highest.
The potential for counterintuitive contributions under layered methods
Another challenge of layered methods is that the changes in employer contribution rates aren’t necessarily related to the funded status or returns at the time. Contribution rates may move in counterintuitive ways, based on what happened 15, 20, or even 30 years ago, depending on the amortization period.
An example in Figure 4 above of contribution rates moving counterintuitively is when contributions rates increase almost 10% from years 34 through 37 under Layered-30. During these same years, returns are quite high, and every other method experiences a decrease in the contribution rate, with contribution rate decreases ranging from 5% under Rolling-30 to 20% under Layered-20.
Another example occurs in years 20 to 23, where all methods except Layered-15 have decreases in employer contributions. The increases in employer contributions under Layered-15 are due to the two years of favorable asset experience in years 4 and 5. Using smoothed assets means significant gains in the few years after that. As those layers peel away, the contribution rates increase.
The rolling periods bear a consistent relationship between the contribution rates and funded status, almost mirroring each other. The better the funded status, the lower the contribution rate. However, the relationship between funded status and contribution rates is not so strict with layered amortizations.
Figure 6: Funded status and employer contributions under Layered-20 (500th scenario)
In Figure 6, the funded status and employer contributions under Layered-20 are shown to illustrate the nature of this relationship.
From years 6 through 10, the employer contributions are zero (a contribution “holiday”). The employer contribution rates then increase from years 11 through 19. In year 20, the initial layer drops off, leading to a drop in the employer contributions from 17% of pay to 7% of pay. This occurs even though the funded status is 73%, well below 100%. This drop may seem counterintuitive to employers when the funded status is low and following nine years of increases in contribution rates. To add to the whiplash, after a couple of years of decreases, the contribution rates begin to increase again in year 23 rising to a peak of 42% of pay in year 29. This volatility in employer contributions may be difficult for plan sponsors to manage.
In contrast, the graph in Figure 7 below, shows the funded status and employer contributions under Rolling-15. Here the employer contributions behave intuitively based on the funded status. When funded status improves, employer contribution rates decrease and vice versa. Instead of a 10% decrease beginning in year 20, there is only a 3% decrease, from 19% of pay in year 20 to 16% of pay in year 22. This more closely mirrors the small increase in funded status during these years.
Figure 7: Funded status and employer contributions under Rolling-15 (500th scenario)
Some stakeholders may prefer that contribution rates are not strictly linked to asset performance or current funded status. After all, budgets may be tighter at the same time that investment markets have suffered losses. While this may be the case, there are better ways to approach this issue than allowing the contribution rate to fluctuate based on experience that is 15, 20, or 30 years old. For instance, employers could contribute to a reserve fund when able to contribute more than the actuarially determined contribution and draw upon the reserve fund at other times.
The path matters
The order of investment returns can play a key role in the funded status and contribution requirements. The scenarios immediately above and below the median scenario (in terms of cumulative asset returns) show radically different paths for funded status and contribution requirements despite having nearly identical aggregated returns over the period.
Which amortization method would best support the goals of the plan’s stakeholders?
In the graphs below, the funded status under different methods moves similarly, as also seen in the median scenario studied. When near 100% funded, there is consistency among the different methods. However, as the funded status moves away from 100% the methods begin to differentiate. In each of these three scenarios, layered methods with shorter amortization periods end the 40-year projection horizon with the highest funded statuses.
There is not as much differentiation in employer contributions in the graphs below, compared to the median scenario studied. Consistent with the median scenario, contributions under rolling methods move together, and are generally less volatile, while contributions under layered methods are more volatile.
Figure 8: Funded status (501st scenario)
Figure 9: Employer contributions (501st scenario)
Figure 10: Contribution rates (501st scenario)
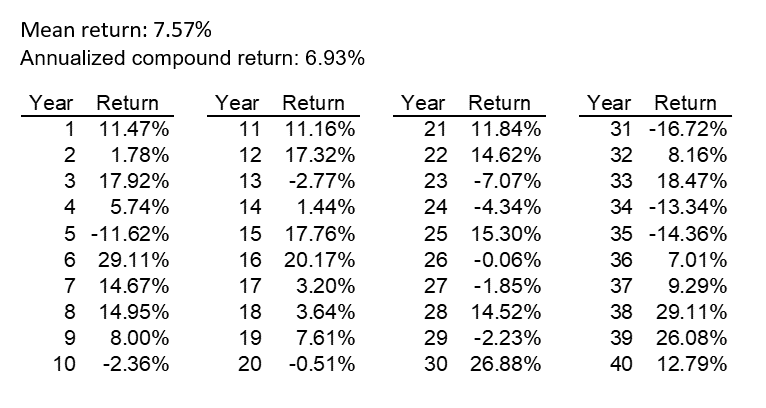
Figure 11: Funded status (499th scenario)
Figure 12: Employer contributions (499th scenario)
Figure 13: Contribution rates (499th scenario)
Volatility in employer contributions
Because volatility in employer contributions can be a particular area of concern for some employers, we highlighted the employer contributions for all three scenarios. We first compare Layered-15 to Rolling-15.
Figure 14: Employer contributions – Layered-15 and Rolling-15
Under layered methods, as time passes, each individual layer gets shorter, and therefore the effective amortization period for a layered amortization will tend to be lower than a rolling amortization with the same “length.” For this reason, it might make more sense to compare Layered-20 to Rolling-15.
Figure 15: Employer contributions – Layered-20 and Rolling-15
Employer contributions when using layered methods are more volatile, with higher peaks under all three scenarios shown.
Summary
In this article we examined how the various amortization methodologies react to the volatility inherent in investment markets, with a focus on the path of single scenarios. The path of a single scenario can be quite volatile and provides insight into how the various amortization methods handle asset volatility.
Under all three scenarios shown, the average return effectively met assumptions. However, the order of investment returns had a significant impact on the funded percentage and especially the employer contributions during the 40-year projection horizon.
Under a single scenario, the various amortization methods led to funded statuses that moved similarly over time, but the employer contribution rates show striking differences between methods, particularly in the second half of the projection.
The rolling periods bear a consistent relationship between the contribution rates and funded status, almost mirroring each other. The better the funded status, the lower the contribution rate. Shorter amortization periods are more responsive, while longer amortization periods have less contribution volatility. The relationship between funded status and contribution rates is not so strict with layered amortizations and can be counterintuitive, given the nature of layered amortization methods on contributions. Rolling methods, in contrast, respond to market events as expected and have lower levels of volatility in employer contributions.
While this article outlines some of the limitations of layered amortization methods, future articles will examine alternative funding policies that incorporate its advantages while partially mitigating some of the contribution volatility.
Although there are limitations to layered amortization methods, rolling amortization methods also present concerns. In many situations, plans with rolling amortization methods are more likely to have a “depletion date” under Governmental Accounting Standards Board (GASB) Statements No. 67 and 68. When a rolling amortization is used with a target of 100% funding, the net pension liability is never fully paid if assumptions are precisely met. Whereas, under a layered methodology, 100% funding will eventually be achieved if all assumptions are precisely met. While we know that assumptions will never be precisely met, there can be negative consequences to having a depletion date under GASB 67/68.
The most appropriate amortization method for a plan will be based on the needs of the stakeholders.
In upcoming articles we’ll explore the cones of uncertainty, a further examination of the depletion date, and other funding policies that will provide alternative options to the methodologies examined in this article.
Appendix: Key methods, provisions, and assumptions
Projections
Assets: Assets are valued based on their fair value, with a five-year smoothing of all fair value gains and losses, except where noted. The expected return is determined for each year based on the beginning-of-year fair value and actual cash flows during the year. Any difference between the expected fair value return and the actual fair value return is recognized evenly over a period of five years.
Initial asset values are such that the funded status of the plan at the beginning of the projection period is 79%.
Investment earnings: Stochastic projections over the 40-year period were generated using a normal distribution, a 7.00% geometric average annual return, and a standard deviation of 12.00%. The equivalent average arithmetic return is 7.72%.
We generated 1,000 scenarios. The median annualized compound return over the 40-year period is 6.93%. The mean annualized compound return over the 40-year period is 7.00%.
Actuarial cost method: Liabilities are valued using the entry age actuarial cost method.
Data: The population is made up of 50% active members, 15% terminated vested members, and 35% retired and in-pay members. Within each status group, males and females are equally weighted by count.
The population is not assumed to grow or decline. Future members are assumed to have the same ages at entry and distribution by sex of the present members that they replace.
Plan provisions: Normal retirement benefits are equal to 2% of the highest consecutive three years of pay per year of service, up to 30 years. Normal retirement benefits are payable at age 65. Upon retirement, benefits increase annually at 2%.
Early retirement benefits and optional forms of benefits are actuarially equivalent to the normal form of payment.
Year-over-year returns
We highlighted several scenarios. We ordered the scenarios from lowest to highest based on the annualized compound return over the 40-year period and defined the “median” as the 500th scenario. We then highlighted the two scenarios closest to this median scenario (the 499th and 501st scenarios). The returns by year under these scenarios are in the tables below.
500th (median) Scenario Returns
499th Scenario Returns
501st Scenario Returns
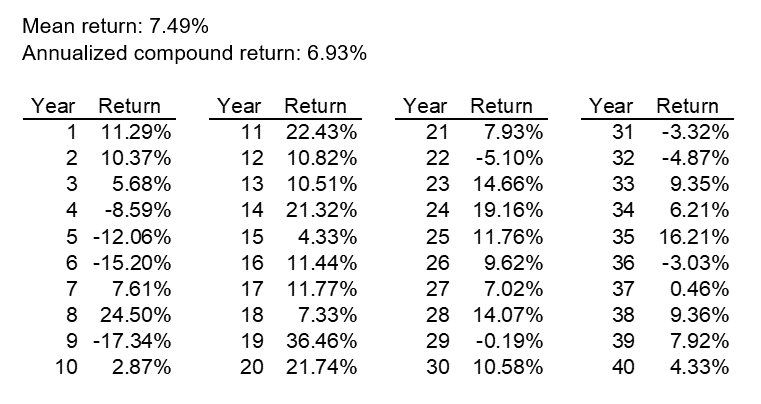
Valuation assumptions
Contributions
- Member contributions: Employee contributions are 6% of pay annually, regardless of the funded status of the plan.
- Employer contributions: Service cost plus amortization of Net Pension Liability (NPL) minus employee contributions, but not less than zero. Note that for the aggregate actuarial cost method, the service cost is defined under that actuarial cost method, and there is no component for the amortization of the NPL.
Demographic assumptions
- Mortality: PubG-2010 general amount-weighted mortality rates projected with MP-2019.
- Termination: Service-based rates starting at 20% in the first year of service and grading to 1.5% at 22 or more years of service.
- Retirement: Rates vary by age and service based on retirement eligibility up to 100% at ages 70 or older.
- Disability: Age-based rates starting at 0% and grading to 0.1% at retirement eligibility.
- Discount rate: Based on a 7.0% annual investment return.
- Projected payroll increases: Total plan payroll increases by 3.0% per year. Individual members receive increases due to promotion and longevity.
Defined terms
Actuarial value of assets: The actuarial value of assets is a smoothed asset value, based on the market value of assets, but recognizing gains and losses over five years.
Amortization methods: Closed, layered, and open/rolling
- Closed amortization methods: Under a closed amortization method, the entire net pension liability is amortized by a specific date. Each year after the actuarial valuation, the remaining number of years over which to pay the net pension liability decreases by one year.
- Layered amortization methods: Under the layered method, an additional layer of amortization is calculated each year based on the experience or assumption changes made that year. Each year the remaining number of years over which to pay each individual layer decreases by one year.
- Rolling amortization methods: Under a “rolling” method the amortization is reset annually based upon the entire net pension liability.
Contribution rates: The percentage of salary contributed to pay for pension benefits. Typically, actuarially calculated contribution rates are comprised of two pieces. The first piece is equal to the service cost and the second is an amortization of the difference between the current funded status of the plan and the target funded status. The target funded status is usually 100%, the point where the net pension liability is zero, where the actuarial value of assets is equal to the total pension liability.
Funded status: The ratio of the assets to the measured liabilities.
GASB: Governmental Accounting Standards Board.
Individual entry age actuarial cost method: The individual entry age actuarial cost method assigns the expected cost of benefits to the years of service for each individual covered by the pension plan. This is the only actuarial cost method permissible for financial reporting under current standards of the GASB. Under this method, a service cost is calculated based on the percentage of pay required to fund contributions, if all actuarial assumptions were exactly realized from hire date until retirement date. The total pension liability is the share of the actuarial present value of benefits assigned to past service based on prior service costs.
Median: The midpoint of a frequency distribution of observed values. The median value of a data set means that half of the values are larger and half are smaller than the median.
Stochastic modeling (Monte Carlo analysis): “Stochastic testing” involves using a random number generator to perform a statistical analysis where 1,000 or more runs are created to test the likelihood of future events. This is also sometimes referred to as Monte Carlo analysis.
1 As an example of how common benefit improvements are when funded statuses are high, we look back to the last time that funded statuses were as high as 120%, just before the dot-com bust of 2000-2002. Consider findings of a survey conducted by the Wisconsin Legislative Council, the "2002 Comparative Study of Major Public Retirement Systems." The report compared significant features of major state and local public employee retirement systems in the United States. The report considered retirement benefits provided to general employees and teachers. According to the survey, 30 of 85 plans increased their benefit multipliers between 2000 and 2002. In addition, 32 of the 85 plans studied increased their benefit multipliers between 1996 and 2000 (some appeared both times).













